Derivative Of Arctan

Posted By admin On 15.09.21

What is the derivative of #y=arctan(cos(x))#?

Derivative Of Arctan(y/x)
Derivative Of Arccos
Derivative Of Arctan(1/x)
Derivative Of Arctan(2x)

Calculate the derivative of the function (y = arccos x arctan x ) at (x = 0. ) Example 9 Using the chain rule, derive the formula for the derivative of the inverse sine function.
Find the Derivative - d/dx arctan(xy) Differentiate using the chain rule, which states that is where. Tap for more steps. To apply the Chain Rule, set as.

1 Answer

Jun 13, 2018 d/dx arctan(1/x) = -1/(x^2+1) We seek: d/dx arctan(1/x) Using the standard result: d/dx tanx=1/(1+x^2) In conjunction with the power rule and the chain rule we get: d/dx arctan(1/x) = 1/(1+(1/x)^2) d/dx (1/x) ' ' = 1/(1+1/x^2) (-1/x^2) ' ' = -1/((1+1/x^2)x^2) ' ' = -1/(x^2+1) Observation: The astute reader will notice that: d/dx arctan(1/x) = -d/dx arctan x From which we conclude that. The Derivative of Arctan X; y = tan−1 x tan y = tan(tan−1 x) tan y = x. So, we’re gonna. Let, the derivative of y = arctan of x. Y’ = 1/(1+x 2) and now we apply the function of tan to both sides to get tan y equals. Tan of arctan of X but tan and arctan. Inverse functions. So, they cancel out so, we get tan of y equals x and now we.

Paul Belliveau · Amory W.

This is a case of knowing the how the derivative of inverse tangent works, and then following the chain rule.

If we were looking at #y=arctan(x)#, there's a way to determine the derivative if you've forgotten the formula.

First remember that #arctan(x)# means 'inverse tangent of x,' sometimes written as #tan^(-1)(x)#. To invert means to switch the x and the y (among other things, but that's the important meaning here).

So #y=tan^(-1)(x)# means the same thing as

#x=tan(y)#

Notice the tangent is no longer an inverse after the switch.

Now we can use implicit differentiation. That's where we don't care whether or not we're looking at a function, that is, we don't care if we have y on one side and everything else on the other. We just derive everything as we go along, and we write #dy/dx# after every term that contains a y (that's a very, very over-simplified explanation of implicit differentiation, but it will work for this problem).

So we derive

#x=tan(y)#

and we get

#1=sec^2(y) dy/dx#

which is the same as

#dy/dx=cos^2(y)#

Which seems straightforward enough. Except for one thing. We don't usually have derivatives that still have y's in them. Not in the first year of Calculus, anyway. We should get rid of that y.

We can go back to a right triangle here. We started with #x=tan(y)#. Than means that there is a right triangle somewhere where the angle is y and the tangent of that angle is x, or #x/1#.

So:

Then by the Pythagorean Theorem, the hypotenuse can be found:

#a^2+b^2=c^2#

#1^2+x^2=c^2#

#c=sqrt(1+x^2)#

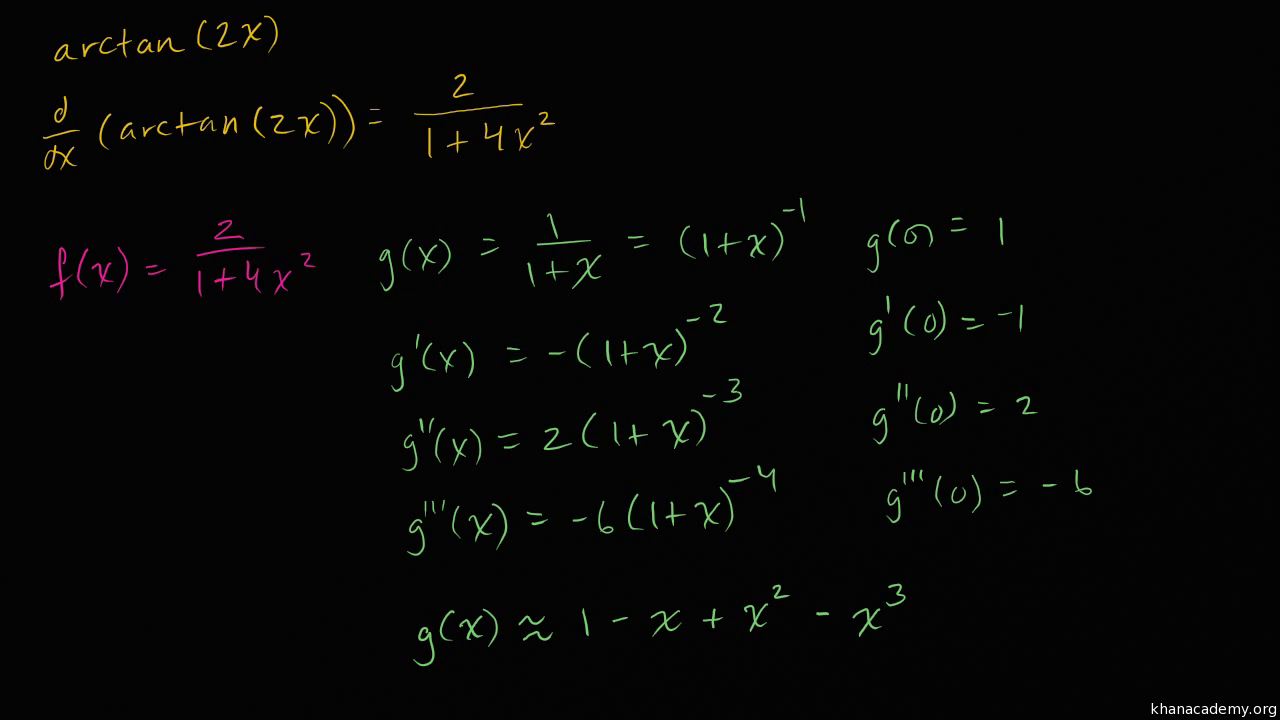
So the #cos(y)=1/sqrt(1+x^2)#

meaning that if

#y=tan^(-1)(x)#

then

#dy/dx=cos^2(y)#

which is the same as

#dy/dx=1/(1+x^2)#

So if we're looking at #y=arctan(cos(x))#, then we apply the derivative rule above, with the chain rule.

The chain rule say that if you have an 'inside function' and an 'outside function,' then you take the derivative of the outside function, and multiply that by the derivative of the inside function, or

If #y=f(g(x))#

#dy/dx=f'(g(x))g'(x)#

Notice the inside function does not change when you derive the outside function.

If #y=arctan(cos(x))#, then my outside function is #y=arctan(x)# (and now we know that derivative). My inside function is #cos(x)#.

Finally:

#y=arctan(cos(x))#

#dy/dx=1/(sqrt(1+(cos(x)^2))) (-sin(x))#

since the derivative of #cos(x)# is #-sin(x)#.

Written more simply,

#dy/dx= (-sin(x))/(sqrt(1+cos^2(x)))#

Hope this helps.

Formula

$dfrac{d}{dx}{, tan^{-1}{x}} ,=, dfrac{1}{1+x^2}$

Introduction

The inverse tangent function is written as $tan^{-1}{x}$ or $arctan{(x)}$ in inverse trigonometry, where $x$ represents a real number. The derivative of the tan inverse function is written in mathematical form in differential calculus as follows.

$(1) ,$ $dfrac{d}{dx}{, Big(tan^{-1}{(x)}Big)}$

$(2) ,$ $dfrac{d}{dx}{, Big(arctan{(x)}Big)}$

The differentiation of the inverse tan function with respect to $x$ is equal to the reciprocal of the sum of one and $x$ squared.

$implies$ $dfrac{d}{dx}{, Big(tan^{-1}{(x)}Big)}$ $,=,$ $dfrac{1}{1+x^2}$

Alternative forms

The differentiation of the tan inverse function can be written in terms of any variable. Here are some of the examples to learn how to express the formula for the derivative of inverse tangent function in calculus.

$(1) ,$ $dfrac{d}{dy}{, Big(tan^{-1}{(y)}Big)}$ $,=,$ $dfrac{1}{1+y^2}$